河南理工大学第三次公开课

发表于 | 本文总阅读量 次

河南理工大学第三次公开课

图片

素数

什么是质数

质数定义为在大于1的自然数中，除了1和它本身以外不再有其他因数。

基本思想找质数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <bits/stdc++.h> // 万能头文件

using namespace std;

int main() {
	
	int n ;
	scanf("%d",&n) ;
	
	if( n == 1 ) {
		printf("false") ;
		return 0;
	}

	for (int i = 2 ; i <= n - 1; i ++ ) {
		if ( n % i == 0 ) {
			printf("fasle") ;
			return 0;
		}
	}
	
	printf("true") ;
	
	return 0;
}

万能头文件

时间小优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>

using namespace std;

int main() {
	int t ; scanf("%d",&t) ;
	
	if ( t == 1 ) {
		printf("false") ;
		return 0;
	}
	
	for (int i = 2 ; i * i <= t ; i ++ ) {
		if ( t % i == 0 ) {
			printf("false") ;
			return 0;
		}
	}
	
	printf("true") ;
	return 0;
}

但是上面两种方法有个很大的弊病，就是不能一次筛出很多素数，加入我们要筛出(1~1e5)之间的所有素数，上面两种方法就很慢了，时间复杂度是O(n^2)

普通筛——埃拉托斯特尼(Eratosthenes)筛法

图片

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
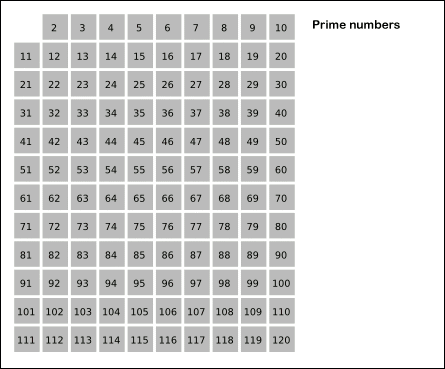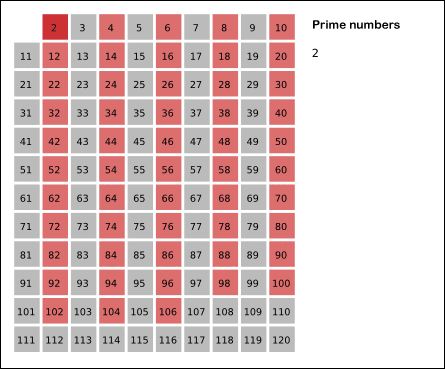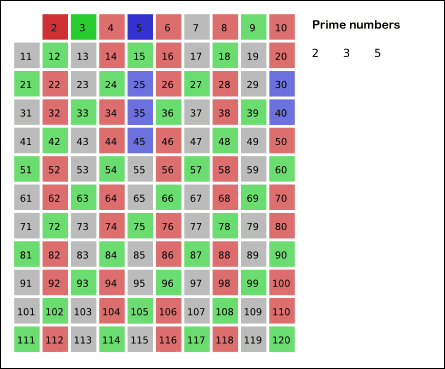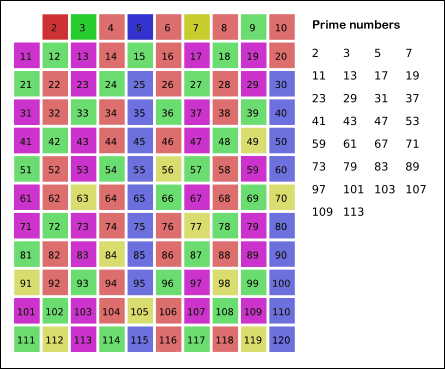
#include <bits/stdc++.h>

using namespace std;

const int maxn = 1e5 + 50 ;

bool prime[maxn] ;

void init() {
	memset(prime ,true ,sizeof(prime)) ;
	prime[1] = prime[0] = false ;
	for (int i = 2 ; i < maxn ; i ++ ) {
		for (int j = 1 ; i * j < maxn ; j ++ ) {
			prime[i*j] = false ;
		}
	}
}

int main() {
	init() ;
	int t ; scanf("%d",&t) ;
	printf("%d\n",prime[t] ) ;
	
	return 0;
}

例题

大神筛法–欧拉筛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
bool IsPrime[1000010];  
int Prim[1000010];  
int  euler_prime(int n){  
    int num = 0, j;  
    for(int i = 2; i <= n; i ++){  
        if(!IsPrime[i])  
            Prim[num ++] = i;  
        for(j  = 0; j < num; j ++){  
            if(i * Prim[j] > n)  
                break;  
            IsPrime[i * Prim[j]] = true;  
            if(i % Prim[j] == 0)  
                break;  
        }  
    }  
}/*欧拉筛*/

图片

扩展

算术基本定理

快速幂

求 a^b 朴素算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <bits/stdc++.h>

using namespace std;

int main() {
	int a ,b ,res = 1 ;
	
	scanf("%d %d",&a ,&b) ;
	
	for (int i = 1 ; i <= b ; i ++ ) {
		res = res * a ;
	}
	
	printf("%d\n",res) ;
	
	return 0;
}

当b为1e9的时候在1s的时间内程序是远远计算不出来的，因此我们需要改进算法
例如5^10 , 10 的二进制表示为 1010

5^10 = 5^(2^2+2^8)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <bits/stdc++.h>

using namespace std;

typedef long long ll ;
const ll mod = 1e9 + 7 ;

ll ksm(ll a ,ll b ) {
	ll res = 1 ;
	while ( b ) {
		if ( b & 1 ) res = res * a % mod ;
		b >>= 1 ;
		a = a * a ;
	}
	return res ;
}

int main() {
	
	printf("%lld\n",ksm(2 ,100 )) ;
	return 0;
}

时间复杂度O(n*lgn)

模

费马小定理

费马小定理(Fermat’s little theorem)是数论中的一个重要定理，在1636年提出。如果p是一个质数，而整数a不是p的倍数，则有a^（p-1）≡1（mod p）。

逆元

大佬博客

当求解公式：(a/b)%m 时，因b可能会过大，会出现爆精度的情况，所以需变除法为乘法：
设c是b的逆元，则有bc≡1(mod m)；
则(a/b)%m = (a/b)1%m = (a/b)bc%m = ac(mod m);
即a/b的模等于ab的逆元的模；

费马小定理+快速幂求逆元
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <bits/stdc++.h>

using namespace std;

typedef long long ll ;
const int maxn = 1e5 + 50 ;
const int mod = 1e9 + 7 ;

ll ksm(ll a ,ll b ) {
	ll res = 1 ;
	while ( b ) {
		if ( b & 1 ) res = res * a % mod ;
		b >>= 1 ;
		a = a * a % mod ;
	}
	return res ;
}

ll inv(ll s) {
	return ksm(s ,mod-2 );
}

int main() {
	ll t ; scanf("%lld",&t) ;
	printf("%lld\n",inv(t) ) ;
	
	return 0;
}

利用逆元求组合数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll ;
const ll mod = 1e9 + 7 ;
const int maxn = 1e6 + 50 ;

ll fac[maxn] ;

void init() {
    fac[1] = 1 ;
    for (int i = 2 ; i < maxn ; i ++ ) {
        fac[i] = (fac[i-1] * i) % mod ;
    }
}

ll ksm(ll a,ll b) {
    a %= mod ;
    ll res = 1 ;
    while(b) {
        if ( b ) res = (res * a) % mod ;
        b /= 2 ;
        a = (a * a ) % mod ;
    }
    return res ;
}

ll inv(ll a) {
    return ksm(a ,mod - 2) ;
}

ll C(ll n ,ll m ) {
    return fac[n] * inv(fac[n-m]) % mod * inv(fac[m]) % mod ;
}


int main() {
	
	return 0 ; 
}

扩展gcd求组合数

扩展gcd

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll ;
const ll mod = 1e9 + 7 ;
const int maxn = 1e6 + 50 ;

ll fac[maxn] ;

void init() {
    fac[1] = 1 ;
    for (int i = 2 ; i < maxn ; i ++ ) {
        fac[i] = (fac[i-1] * i) % mod ;
    }
}

//利用扩展gcd求逆元 
ll ex_gcd(ll a ,ll b ,ll &x ,ll &y ){
	if( b == 0 ){
		x = 1 ;
		y = 0 ;
		return a ;
	}
	int ans = ex_gcd(b ,a%b ,y ,x );
	y -=  x * (a / b);
	return ans;
}

ll inv(ll n){
	ll x ,y ;
	ex_gcd(n ,mod ,x ,y );
	x = (x % mod + mod ) % mod ;
	return x ;
}

ll C(ll n ,ll m ) {
	return fac[n] * inv(fac[n-m]) % mod * inv(fac[m]) % mod ;
}

int main() {
	
	return 0 ; 
}

扩展

卢卡斯定理

图片